Penyelesaian:
·
Himpunan
Z merupakan himpunan tak kosong
Z = { ... , -2, -1, 0, 1, 2, ... }
Karena 0 ϵ Z maka Z ≠ Ø
·
Bersifat
tidak tertutup
Untuk setiap a, b ϵ Z → a + 1/b Ɇ Z
Karena
a ϵ Z
1/b Ɇ Z
Misal, a = 2, b = 3 maka 2 +
1/3 = 7/3 Ɇ Z.
Jadi dapat disimpulkan bahwa operasi ° pada Z bukan merupakan operasi biner.
b. Bersifat asosiatif
Sifat asosiatif
: (a ° b) ° c = a ° (b ° c) a, b, c ϵ Z.
1)
(a °
b) ° c = (a + 1/b) ° c
= (a + 1/b) + c
= a + 1/b + c
2)
a °
(b ° c) = a ° (1/b + c)
= a + (1/b + c)
= a + 1/b + c
Misal a = 1, b = 2, c = 3 maka
(a + 1/b) + c = a + (1/b + c)
(1 + ½) + 3 = 1 + (1/2 + 3)
9/2 =
9/2
Jadi operasi ° terbukti memenuhi sifat asosiatif.
c. Mempunyai elemen identitas
a ϵ Z maka a ° e = e ° a = a
1) a ° e = a + 1/e = a
e
= 1
2) e ° a = 1/e + a = a

e = 1
Jadi operasi ° pada Z memiliki elemen identitas yaitu 1.
d. setiap elemen di Z mempunyai identitas
a ϵ Z maka a ° a¯¹ = a¯¹ ° a = e
1)
a °
a¯¹ = e
a + (1/a)¯¹ = 1
a¯¹ = a – 1
2)
a¯¹
° a = e
(1/a)¯¹ + a = 1
a¯¹ = a - 1
Jadi a ° a¯¹ = a¯¹ ° a = e yaitu a¯¹ = a – 1
e. bersifat komutatif
sifat komutatif a ° b = b ° a, a, b ϵ
Z.
1)
a °
b = a + 1/b
2)
b °
a = b + 1/a
misal, a =1, b = 2 maka
1)
a °
b = 1 + ½ = 3/2
2)
b °
a = 2 + 1/1 = 2
Jadi operasi ° tidak memenuhi sifat
komutatif.
Penyelesaian:
a. Merupakan operasi biner
·
Himpunan
Z merupakan himpunan tak kosong
Z = { ... , -2, -1, 0, 1, 2, ... }
Karena 0 ϵ Z maka Z ≠ Ø
·
Bersifat
tertutup
Untuk setiap a, b ϵ Z → a + 2b ϵ Z
Karena a ϵ Z dan b ϵ Z
Misal a = 3, b = 2 maka
a + 2b = 3 + 2(2) = 7 ϵ Z
Jadi operasi ° pada Z merupakan operasi biner.
b. Bersifat asosiatif
Sifat asosiatif : (a ° b) ° c = a ° (b ° c) a, b, c ϵ Z.
1) (a ° b) ° c = (a + 2b) ° c
= a + 2b + c
2) a ° (b ° c) = a ° (b + 2c)
= a + (b + 2c)
Jadi operasi ° pada Z bukan bersifat asosiatif.
c. Mempunyai elemen identitas
a ϵ Z maka a ° e = e ° a = a
1) a ° e = a + 2e = a
2e = a – a
e
= 0/2
e = 0
2) e ° a = 2e + a = a
2e = 0
e =
0/2
e =
0
jadi operasi ° pada Z memiliki elemen identitas yaitu 0.
d. setiap elemen di Z memiliki elemen identitas
a ϵ Z maka a ° a¯¹ = a¯¹ ° a = e
1) a ° a¯¹ = e
a + (2a)¯¹ = 0
a¯¹ = a/2
2) a¯¹ ° a = e
(2a)¯¹ + a = 0
a¯¹ = a/2
Jadi a ° a¯¹ = a¯¹ ° a = e yaitu a¯¹ = a/2
e. Bersifat komutatif
Sifat komutatif a ° b = b ° a, a, b ϵ Z.
1) a ° b = a + 2b
2) b ° a = b + 2a
misal, a = 2, b = 3.
1) a ° b = 2 + 2 (3) = 8
2) b ° a = 3 + 2 (2) = 7
Jadi operasi ° pada Z bukan bersifat
komutatif.
a. Merupakan operasi biner
Himpunan matriks M, dengan setiap elemennya bilangan rasional .
Ambil sembarang M₁, M₂ ∊ M
Jadi untuk setiap M₁, M₂ ∊ M, ada M = M₁ x M₂ ∊ M atau tertutup terhadap operasi perkalian ( merupakan operasi biner ).
b. Bersifat asosiatif
Jadi operasi tersebut bukan besifat asosiatif.
c. Bersifat komutatif
Jadi operasi tersebut tidak besifat komutatif
d. Mempunyai elemen identitas
M x e = e x M = M
Misalkan elemenya e = ɵ maka :
SEMOGA BERMANFAAT ☺☺☺☺


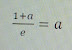



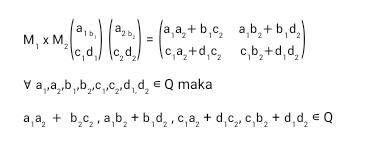








Tidak ada komentar:
Posting Komentar