Salah satu hal yang dipelajari pada matematika adalah fungsi. Pada dasarnya fungsi merupakan suatu relasi yang memetakan setiap anggota sebuah himpunan yang disebut sebagai daera asal atau domain ke tepat satu anggota himpunan lain yang disebut daerah kawan (kodomain). Pada artikel sebelumnya saya telah membahas sedikit mengenai himpunan. Berikut ini jenis-jenis fungsi:
Jenis - Jenis Fungsi
1. Fungsi Identitas
Dalam
matematika, fungsi identitas, disebut juga relasi identitas, pemetaan identitas
atau transformasi identitas, adalah fungsi yang selalu menghasilkan nilai yang
sama dengan yang diberikan atau dimasukkan. Agar f menjadi fungsi identitas,
persamaan f(x) = x harus terpenuhi semua x.
Defenisi
Suatu
fungsi f(x) disebut fungsi identitas apabila setiap anggota domain fungsi
berlaku f(x) = x atau setiap anggota domain fungsi dipetakan pada dirinya
sendiri.
Grafik
fungsi identitas berupa garis lurus yang melalui titik asal dan semua titik
absis maupun ordinatnya sama. Fungsi identitas ditentukan oleh f(x) = x. Agar
lebih memahami tentang fungsi identitas berikut contoh dari fungsi identitas.
Contoh
Fungsi Identitas
Fungsi pada R didefinisikan sebagai
f(x) = x untuk setiap x.
a. Carilah f(–2), f(0), f(1), f(3).
b. Gambarlah grafiknya.
Penyelesaian:
a. Nilai f(–2), f(-1), f(1), dan f(3).
f(x) = x
f(–2) = –2
f(-1) = –1
f(1) = 1
f(3) = 3
Misalkan
f merupakan fungsi dari A ke B maka f disebut Fungsi surjektif jika
setiap unsur B di kodomain maka selalu terdapat unsur dalam A.
Defenisi
:
Misalkan
A dan B adalah himpunan, dan f adalah fungsi dari A ke B. Fungsi f disebut
fungsi pada jika R(f) = B. Jadi, f : A→B disebut fungsi pada jika untuk
masing-masing y ∈ B dan x ∈ A sehingga f (x) = y . Fungsi surjektif sering disebut juga dengan
fungsi pada atau fungsi onto. Jika f fungsi surjektif, maka f disebut surjeksi
(Bartle danSherbert, 2000:8).
Pemetaan
(fungsi) f : A B dikatakan Surjektif, jika untuk setiap
unsur y B terdapat unsur x A yang memenuhi f(x) = y.
Suatu
fungsi/pemetaan f disebut pemetaan onto/kepada (surjektif) bila dan hanya bila ∀ y ∈ B, ∃ x ∈ A ∋
f(x) = y
Ciri
khusus dari Fungsi surjektif adalah Rf = B
atau Kodomain sama dengan Daerah Hasil. Perhatikan gambar
diagram pemetaan dibawah ini :
Keterangan :
Gambar diagram pemetaan pertama atau
sebelah kiri merupakan fungsi surjektif karena setiap anggota di
kodomain terdapat pasangan di domain.
f : A → A, dengan f(x) :=
x²,
untuk mengecek apakah f(x) merupakan Fungsi surjektif atau bukan, pertama kita harus menerka / menebak, jika fungsi tersebut bukan merupakan Fungsi surjektif, kita bisa memberikan contoh yang tidak memenuhi Definisi Fungsi surjektif.
Misal kita ambil x = -1, 0 dan 1
f(-1) = (-1)² = 1
f(0) = (0)² = 0
f(1) = (1)² = 1
Karena terdapat anggota kodomain yaitu f(x) = -1 yang tidak memiliki kawan di domain, sehingga f bukan Fungsi surjektif.
Contoh 2
g : A → A, dengan g(x) =
x³
ambil y → A (kodomain)
sebarang dan g(x) = y, berakibat
y = x³
sehingga terdapat x = y⅓ →
A (domain). Berdasarkan Definisi maka fungsi g(x)
merupakan Fungsi surjektif.
Atau kita juga bisa dengan cara
mendaftarkan terlebih dahulu pemetaannya :
g(-1) = (-1)³ = -1
g(0) = (0)³ = 0
g(1) = (1)³ = 1
Rf = {-1, 0, 1}
Karena Rf = B, maka g(x) merupakan Fungsi surjektif.
3. Fungsi injektif
Fungsi
injektif adalah fungsi satu-satu yaitu untuk x₁ ≠ x₂ maka f(x₁) ≠ f(x₂).
Defenisi
Fungsi
f : A => B disebut fungsi injektif atau fungsi satu-satu apabila anggota
yang berbeda di B memiliki pasangan atau kawan yang berbeda di A. hal ini
berarti jika anggota yang berbeda di A tidak boleh memiliki pasangan yang sama
di B.
Contoh
1
Fungsi f: A → B disebut fungsi injeksi jika setiap elemen B memiliki pasangan elemen tepat A. berdasarkan konsep ini, dapat disimpulkan bahwa hanya angka diagram panah (4) yang merupakan fungsi injeksi
4. Fungsi Bijektif (1-1 dan onto)
Fungsi
bijektif adalah fungsi yang injektif sekaligus surjektif. Pada fungsi bijektif,
setiap anggota kodomain mempunyai tepat satu prapeta pada domain.
Definisi
:
Pemetaan (fungsi) f : A → B dikatakan bijektif jika f adalah Fungsi Satu-Satu dan Fungsi Pada.
Fungsi
Bijektif akan terjadi jika jumlah
anggota domain sama dengan jumlah anggota kodomain. Dengan catatan bahwa tidak
ada dua domain berbeda atau lebih dipetakan ke kodomain yang sama dan setiap
kodomain memiliki pasangan di domain.
Keterangan
:
Pemetaan
pertama merupakan Fungsi Bijeksi karena sudah sesuai dengan Difinisi.
Pemetaan
kedua bukan Fungsi Bijeksi karena pada pemetaan tersebut hanya terjadi Fungsi
Pada. Perhatikan “d” dan “e” di domain, kedua anggota domain tersebut dipetakan
ke anggota domain yang sama (lihat Definisi Fungsi Satu-Satu)
Pemetaan
ketiga bukan Fungsi Bijeksi karena pada pemetaan tersebut hanya terjadi Fungsi
Satu-Satu. Karena terdapat anggota kodomain yaitu “9” yang tidak memiliki
pasangan pada anggota domain.
Contoh
Apakah
pasangan berurutan ini F ={(1,a), (2,b), (3, c), (4, d)} merupakan jenis
fungsi bijektif dengan domain Df = {1, 2,
3, 4} dan kodomain Kf = {a, b, c, d}
Jawabannya
:
F =
{(1, a), (2, b), (3, c), (4, d)} , dengan Df = {1, 2, 3, 4} dan Kf = {a, b, c, d}
Jika pasangan berurutan digambar dalam diagram panah , maka:
Syarat
f sebagai fungsi sudah terpenuhi, karena f Memetakkan setiap anggota Df ke
tepat satu anggota Kf.
Karena Range f sama dengan kodomain f ( Rf = Kf ) maka f fungsi onto atau subjektif. Karena setiap anggota Kf tepat berpasangan dengan satu anggota Df maka f merupakan fungsi injektif. Dalam hal ini f = {(1, b), (2, b), (3, b), (4, b)} merupakan fungsi subjektif dan injektif Atau bisa disebut juga fungsi bijektif.
5. Fungsi Invers
Fungsi
invers atau fungsi kebalikan merupakan suatu fungsi yang berkebalikan dari
fungsi asalnya. Fungsi invers adalah fungsi dengan kodomain sebagai masukan dan
domain sebagai hasil masukan. Biasanya fungsi memiliki domain dan kodomain atau
asal dan daerah hasil dengan arah nya adalah domain ke kodomain. Kalo dalam
fungsi invers berbeda. Arah gerak hasilnya adalah kodomain menuju domain.
Penulisan simbol pada fungsi invers dapat dinyatakan sebagai berikut:
(f¯¹)
Ada
3 langkah untuk menentukan fungsi invers, yaitu:
1.
Ubahlah bentuk y = f(x) menjadi bentuk x = f(y).
2.
Tuliskan x sebagai f-1(y) sehingga f-1(y) = f(y).
3.
Ubahlah variabel y dengan x sehingga diperoleh rumus fungsi invers f-1(x).
Dalam
fungsi invers terdapat rumus khusus seperti berikut:
Contoh
Tentukan
rumus fungsi invers dari fungsi f(x) = 2x + 6.
Pembahasan:
demikianlah penjelasan mengenai jenis-jenis fungsi pada matematika.









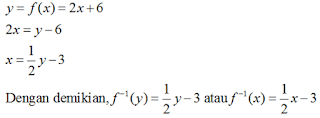




Tidak ada komentar:
Posting Komentar